Name:     ID: 
 
Email: 

U2L4XORandXNORbinaryAdders

Multiple Choice
Identify the choice that best completes the statement or answers the question.
 

 1. 
The Boolean equation for the exclusive-OR function is
a.
X = mc001-1.jpgB + Amc001-2.jpg.
c.
X = mc001-5.jpg mc001-6.jpg + AB.
b.
X = mc001-3.jpgB + mc001-4.jpg.
d.
X = mc001-7.jpg + AB.
 

 2. 
When the inputs to an exclusive-OR gate are the same logic level, the output is
a.
zero.
c.
one.
b.
HIGH.
d.
cannot tell
 

 3. 
During which time interval(s) will output X of this XOR timing diagram be LOW?
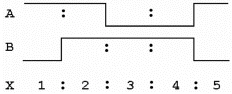
mc003-1.jpg
a.
time interval 1
c.
time intervals 3 and 4
b.
time interval 2
d.
time intervals 4 and 5
 

 4. 
During which time interval(s) will output X of this XOR timing diagram be HIGH?
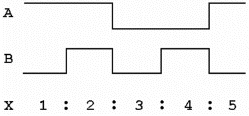
mc004-1.jpg
a.
time intervals 1, 3, and 5
c.
time intervals 2 and 4
b.
time intervals 1, 4, and 5
d.
time interval 3
 

 5. 
What is the correct set of output values for this XOR truth table?

      A      B      X
      0      0     
      0      1
      1      0
      1      1
a.
X =      0
      1
      1
      1
b.
X =      0
      0
      0
      1
c.
X =      0
      1
      1
      0
d.
X =      0
      0
      1
      1
 

 6. 
The Boolean equation for the exclusive-NOR function is
a.
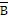X = A + B + mc006-1.jpg + mc006-2.jpg.
c.
X = AB + mc006-4.jpg mc006-5.jpg.
b.
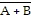X = mc006-3.jpg.
d.
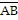X = AB + mc006-6.jpg.
 

 7. 
When the inputs to an exclusive-NOR gate are unequal, the output is
a.
one.
c.
zero.
b.
HIGH.
d.
cannot tell
 

 8. 
During which time interval(s) will output X of this XNOR timing diagram be LOW?
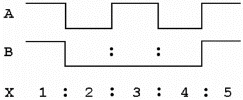
mc008-1.jpg
a.
time intervals 1, 2, 4, 5
c.
time interval 1
b.
time intervals 1 and 5
d.
time interval 3
 

 9. 
During which time interval(s) will output X of this XNOR timing diagram be HIGH?
mc009-1.jpg
a.
time interval 1
c.
time interval 5
b.
time intervals 2, 3, and 4
d.
time intervals 1 and 5
 

 10. 
What is the correct output for this XNOR truth table?

      A      B      X
      0      0
      0      1
      1      0
      1      1
a.
X =      1
      1
      1
      0
b.
X =      0
      1
      1
      0
c.
X =      1
      0
      0
      1
d.
X =      0
      1
      1
      1
 

 11. 
A HIGH output if one or the other inputs is HIGH, but not both; describes a(n) ________ gate.
a.
XNOR
c.
OR
b.
XOR
d.
AND
 

 12. 
If the same signal is connected to both inputs of an XOR gate, the output is
a.
undetermined.
c.
HIGH.
b.
LOW.
d.
a clock waveform.
 

 13. 
Use your two bit adder to do the following binary addition.
   0101
+ 0111
a.
1110
c.
1010
b.
1100
d.
1111
 

 14. 
Use your two bit adder to do the following binary addition.
   0011
+ 1001
a.
1110
c.
1010
b.
1100
d.
1111
 

 15. 
Use your two bit adder to do the following binary addition.
   1001
+ 0101
a.
1110
c.
1010
b.
1100
d.
1111
 

 16. 
Use your two bit adder to do the following binary addition.
   1010
+ 1101
a.
1110
c.
1010
b.
1100
d.
1111
 

 17. 
This is an ___________ logic gate.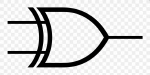
mc017-1.jpg
a.
NOR
c.
XNOR
b.
OR
d.
XOR
 

 18. 
This is an ___________ logic gate.
mc018-1.jpg
a.
NOR
c.
XNOR
b.
OR
d.
XOR
 

Problem
 

 19. 

      Using the Multisim, enter the 2-bit adder shown below. This adder is implemented with SSI logic (i.e., AND gates, OR gates, and XOR gates). 
This circuit has two 2-bit inputs (X1, X0 and Y1, Y0) and three outputs (S2, S1, and S0). S2-S0 is the sum of adding together X1-X0 and Y1-Y0. Additionally, the outputs (S2-S0) are connected to a common anode seven-segment display through a 74LS47 display driver.
Note: The wires are color coded to help with readability; these colors do not need to be maintained in your drawing.
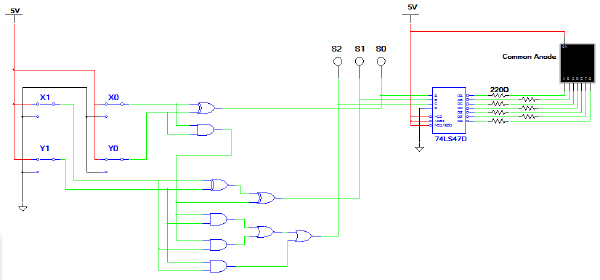
pr019-1.jpg


Verify that the circuit is working as expected by completing the truth table shown. 
Inputs
Outputs
X1
X0
X
Y1
Y0
Y
S2
S1
S0
Display
0
0
0
0
0
0
    
0
0
0
0
1
1
    
0
0
0
1
0
2
    
0
0
0
1
1
3
    
0
1
1
0
0
0
    
0
1
1
0
1
1
    
0
1
1
1
0
2
    
0
1
1
1
1
3
    
1
0
2
0
0
0
    
1
0
2
0
1
1
    
1
0
2
1
0
2
    
1
0
2
1
1
3
    
1
1
3
0
0
0
    
1
1
3
0
1
1
    
1
1
3
1
0
2
    
1
1
3
1
1
3
    

Make sure that you show me your circuit and completed truth table in class.  We may breadboard this circuit. Fill in the answer to this problem with completed in class.
 

 20. 

      Use the Multisim to enter the 2-bit adder shown below. This adder is implemented with 74LS183 MSI full add gates. 
This circuit is functionally identical to the SSI implementation from step number 1.
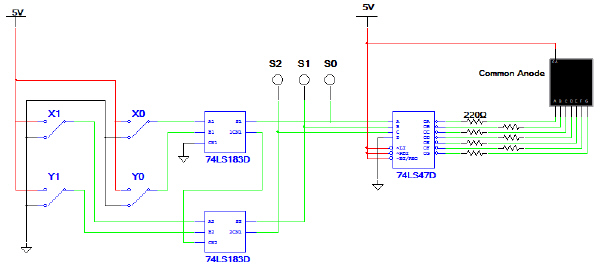
pr020-1.jpg


Verify that the circuit is working as expected by completing the truth table shown.

Inputs
Outputs
X1
X0
X
Y1
Y0
Y
S2
S1
S0
Display
0
0
0
0
0
0
    
0
0
0
0
1
1
    
0
0
0
1
0
2
    
0
0
0
1
1
3
    
0
1
1
0
0
0
    
0
1
1
0
1
1
    
0
1
1
1
0
2
    
0
1
1
1
1
3
    
1
0
2
0
0
0
    
1
0
2
0
1
1
    
1
0
2
1
0
2
    
1
0
2
1
1
3
    
1
1
3
0
0
0
    
1
1
3
0
1
1
    
1
1
3
1
0
2
    
1
1
3
1
1
3
    


Make sure that you show me your circuit and completed truth table in class.  We may breadboard this circuit. Fill in the answer to this problem with completed in class.
 



 
         Start Over