Name:     ID: 
 
Email: 

U2L4TWOsComplementArithmatic

Multiple Choice
Identify the choice that best completes the statement or answers the question.
 

 1. 
The binary addition of 0 + 1 =
a.
sum = 1
carry = 1
b.
sum = 1
carry = 0
c.
sum = 0
carry = 0
d.
sum = 0
carry = 1
 

 2. 
The binary addition of 1 + 0 =
a.
sum = 0
carry = 0
b.
sum = 1
carry = 1
c.
sum = 1
carry = 0
d.
sum = 0
carry = 1
 

 3. 
The binary addition of 1 + 1 =
a.
sum = 1
carry = 0
b.
sum = 0
carry = 1
c.
sum = 0
carry = 0
d.
sum = 1
carry = 1
 

 4. 
The binary addition of 1 + 0 + 0 =
a.
sum = 1
carry = 1
b.
sum = 0
carry = 1
c.
sum = 0
carry = 0
d.
sum = 1
carry = 0
 

 5. 
The binary addition of 1 + 1 + 0 =
a.
sum = 0
carry = 1
b.
sum = 0
carry = 0
c.
sum = 1
carry = 0
d.
sum = 1
carry = 1
 

 6. 
The binary addition of 1 + 1 + 1 =
a.
sum = 1
carry = 1
b.
sum = 1
carry = 0
c.
sum = 0
carry = 1
d.
sum = 0
carry = 0
 

 7. 
Solve this binary problem:      0110
      + 0011
a.
1000
c.
0111
b.
0100
d.
1001
 

 8. 
Solve this binary problem:      1000
      +1001
a.
11001
c.
1111
b.
10001
d.
10111
 

 9. 
Solve this binary problem:      1111
      +1001
a.
1111
c.
11000
b.
11111
d.
10111
 

 10. 
Solve this binary problem:      00010111
      +00101001
a.
00101111
c.
01000000
b.
01100000
d.
00110011
 

 11. 
Solve this binary problem:      0110
      -0010
a.
0110
c.
0100
b.
1000
d.
0011
 

 12. 
Solve this binary problem:      1000
      -0001
a.
1001
c.
0101
b.
0111
d.
0110
 

 13. 
Solve this binary problem:      0011
      -0001
a.
0010
c.
0001
b.
0011
d.
0000
 

 14. 
Solve this binary problem:      1011
      -0101
a.
0101
c.
0110
b.
1010
d.
1000
 

 15. 
Without performing any binary-to-decimal conversions, which of the following binary numbers must be -49?
a.
00110001
c.
11001111
b.
01100110
d.
01001111
 

 16. 
What is the one’s complement of the binary number 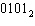mc016-1.jpg
a.
1100
c.
1101
b.
0011
d.
1010
 

 17. 
What is the one’s complement of the binary number 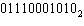mc017-1.jpg
a.
10000000101
c.
10101110110
b.
10001110101
d.
10001110111
 

 18. 
Calculate the 2’s complement of the following binary number:
1001101
a.
0110010
c.
1001110
b.
0110011
d.
0110100
 

Matching
 
 
Match the following decimal numbers as their 8-bit 2’s complement binary equivalent.
a.
grp001-1.jpg
d.
grp001-4.jpg
b.
grp001-2.jpg
e.
grp001-5.jpg
c.
grp001-3.jpg
 

 19. 

 01010111
 

 20. 

 10011111
 

 21. 

 11001111
 

 22. 

 01110010
 

 23. 

 10010100
 
 
Match the following 8-bit 2’s complement binary numbers as their decimal equivalent.
a.
11011001
d.
10111101
b.
01110100
e.
00011011
c.
10110001
 

 24. 

 116
 

 25. 

 -67
 

 26. 

 -79
 

 27. 

 27
 

 28. 

 -39
 



 
         Start Over