Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Using DeMorgan’s Theorems and the other theorems and laws of Boolean
algebra, simplify the following expression: 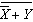
|
|
|
2.
|
Using DeMorgan’s Theorems and the other theorems and laws of Boolean
algebra, simplify the following expression: 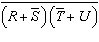
|
|
|
3.
|
Using DeMorgan’s Theorems and the other theorems and laws of Boolean
algebra, simplify the following expression: 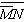
|
|
|
4.
|
Using DeMorgan’s Theorems and the other theorems and laws of Boolean
algebra, simplify the following expression: 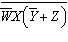
|
|
|
5.
|
Using DeMorgan’s Theorems and the other theorems and laws of Boolean
algebra, simplify the following expression: 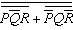 a. | 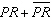 | c. | 0 | b. | 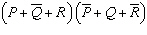 | d. | 1 |
|
|
|
6.
|
Using DeMorgan’s Theorems and the other theorems and laws of Boolean
algebra, simplify the following expression: 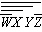
|
|
|
7.
|
The simplest form of X = 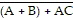 is ________. is ________.
|
|
|
8.
|
What is the simplest form of X
= AB + A + BC? + BC?
a. | X = AB +
C | c. | X = B +
C +
C | b. | X = A +
BC | d. | It is in its simplest
form. |
|
|
|
9.
|
Which of the following is an
example of DeMorgan's theorem?
|
|
|
10.
|
By using DeMorgan's
theorem, X = 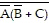 is simplified to
________. is simplified to
________.
a. | X = A(B +  ) ) | c. | X = A + B +  | b. | X = AB | d. | X = A + B |
|
|
|
11.
|
Which step in this reduction
series is based on DeMorgan's Theorem?
X = 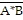 ( (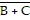 ) STEP 1 X = ( ) STEP 1 X = ( +
+ 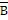 )( )(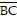 ) )
STEP 2 X =  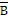  + + 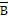
 
STEP 3 X = 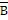  ( ( +
1) +
1)
STEP
4 X = 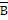 
a. | STEP 1 | c. | STEP 3 | b. | STEP 2 | d. | STEP 4 |
|